主成分分析(PCA)はデータセットの情報を要約して特長量の数を減らす特徴抽出の一つです。 特徴空間を元のデータ構造をできるだけ保ったまま低次元に圧縮して表現できるような座標軸を新たに設定することが目的です。
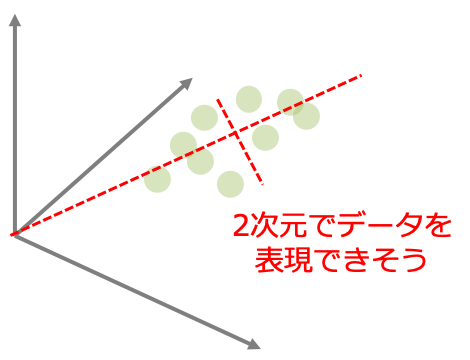
主成分分析のアルゴリズム
主成分分析は以下の手順で処理されていきます。
- データセットを標準化する
- 標準化データの共分散行列を求める
- 共分散行列の固有ベクトルと固有値を求める
- 固有値の大きいk個の固有ベクトルを抽出する
- 抽出した固有ベクトルから射影行列を求め、入力データセットを変換することで新しい特徴(部分)空間を取得する
この説明だけでは全く意味不明だと思うので一つ一つの処理を説明していきます。
目的は分散を最大化する
まず初めに主成分分析の目的は高次元のデータにおいて分散が最大となるような方向(ベクトル$a$)を見つけることです。この目的を踏まえた上で各処理を考えていきます。
ここで目的のベクトル$\bm{a}$を単位ベクトル($\bm{a}^T\bm{a}=1$)という制約を設けます。方向さえ分かればいいので単位ベクトルで構わないというだけの意味です。
前提として対象とするデータセットを以下のように定義します。
$\bm{X}$:対象データのn行d列の行列(n:データ点数、d:特徴量数)$\bm{x}$:$\bm{X}$のある一点のデータ点を表すベクトル
学力の例でいうと$\bm{x}$はある生徒のd科目のテストの点数を表し、各成分は各科目の得点が格納されています。

ベクトル$\bm{x}$を$\bm{a}$上へ射影すると、そのベクトルの長さ$z$(主成分)は以下のように表すことができます。
$$z = \bm{x}^T\bm{a}$$
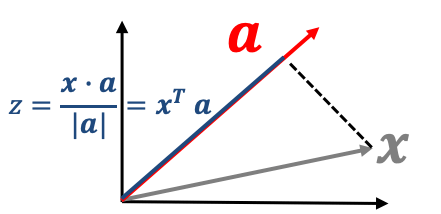
つまり$z$は元々のデータ$\bm{x}$を新しい座標軸$\bm{a}$上に変換した時の原点からの長さを表しています。そこで$z$の分散が最大となるように計算すれば元の情報をなるべく残していると考えることができます。
以上より私たちは$z = \bm{x}^T\bm{a}$の分散を最大化することを考えていきます。
データセットを標準化
主成分分析をするにあたって気をつけなければならないのはデータのスケーリング(尺度)です。特徴量空間では数字にしか意味がありません。
私たちの月給(何十万)という特徴量と年齢(数十)という異なるスケールの特徴量同しを扱うにはデータを標準化する必要があります。
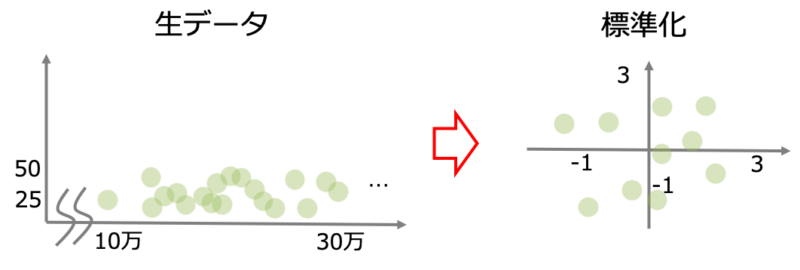
標準化とはばらつきのあるデータの平均が0になるように中心化する処理です。
$$\frac{x-\mu}{s}$$
$\mu$はデータ$x$の平均を、$s$はデータ$x$の標準偏差を表しています。
共分散行列を求める
データを標準化したらまず行うことは共分散行列を求めることです。
共分散行列とは各成分に特徴量$x_i$と$x_j$の共分散$\sigma_{jk}$を持つ行列です。共分散は以下のように定義され、標準化されたデータ($\mu=0$)においては分散と一致します。
$$\sigma_{jk} = \frac{1}{n}\sum^n_{i=1}(x^{(i)}_j – \mu_j)(x^{(i)}_k – \mu_k)$$
なぜ共分散行列を求めるかというと、主成分$z$の分散は共分散行列$C_X$を用いて表現できるからです。
$$\begin{aligned}var(z) &= \frac{1}{n}\sum_i^n (z_i – \mu)^2 \\ &=\frac{1}{n}\sum_i^n (\bm{a}^T\bm{x^{(i)}} – \bm{a}^T\bm{\mu})^2 \\ &= \frac{1}{n}\sum_i^n \bm{a}^T(\bm{x^{(i)}} – \bm{\mu})(\bm{x^{(i)}} – \bm{\mu})^T \bm{a}\\ &= \bm{a}^T \left( \frac{1}{n}\sum_i^n (\bm{x^{(i)}} – \bm{\mu})(\bm{x^{(i)}} – \bm{\mu})^T \right) \bm{a} \\&=\bm{a}^TC_X\bm{a}\end{aligned}$$
共分散行列の固有値問題を解く
上の式からデータの分散が最大となるベクトル$\bm{a}$を求めることは、$\bm{a}^TC_X\bm{a}$を最大化する$\bm{a}$を求めることと等価となります。
この問題は拘束条件$\bm{a}^T\bm{a}=1$の下でのラグランジュの未定乗数法により解くことができます。
ラグランジュ乗数$\lambda$を導入するとラグランジュ関数Lを最大とするような$\bm{a}$を求めます。
$$L = \bm{a}^TC_x\bm{a} – \lambda (\bm{a}^T\bm{a}-1)$$
$L$を$\bm{a}$で微分して0となる停留点が最大値を取り得るので停留点の条件を考えます。
$$\frac{\partial L}{\partial \bm{a}} = 2C_X\bm{a} – 2\lambda\bm{a} = 0$$
つまり
$$C_X\bm{a} = \lamda\bm{a}$$
を解けば良いということです。これは共分散行列の固有値問題そのものです。
固有値の大きいk個の固有ベクトルを抽出する
以上の固有値問題を解いて得られる固有ベクトル$\bm{a}$は特徴量空間において新たな座標軸となりうるベクトルです。そこで十分に情報を表現できるk個だけを新たな特徴部分空間の座標軸として用いることで次元削減を行います。
入力データセットを変換する
新しい座標軸を決定することができたので、元のデータ$\bm{X}$を変換します。
上の処理で選択したk個の固有ベクトルからn×d次元の射影行列$W$が作成できるので、元のデータ$\bm{X}$に作用させることによって新しい特徴部分空間における特徴量$\bm{X’}$を得ることができます。
$$\bm{X’} = \bm{X}\bm{W}$$
以上の処理によって次元削減を行います。これらの処理をpythonで実装して確認しましょう。(別記事)





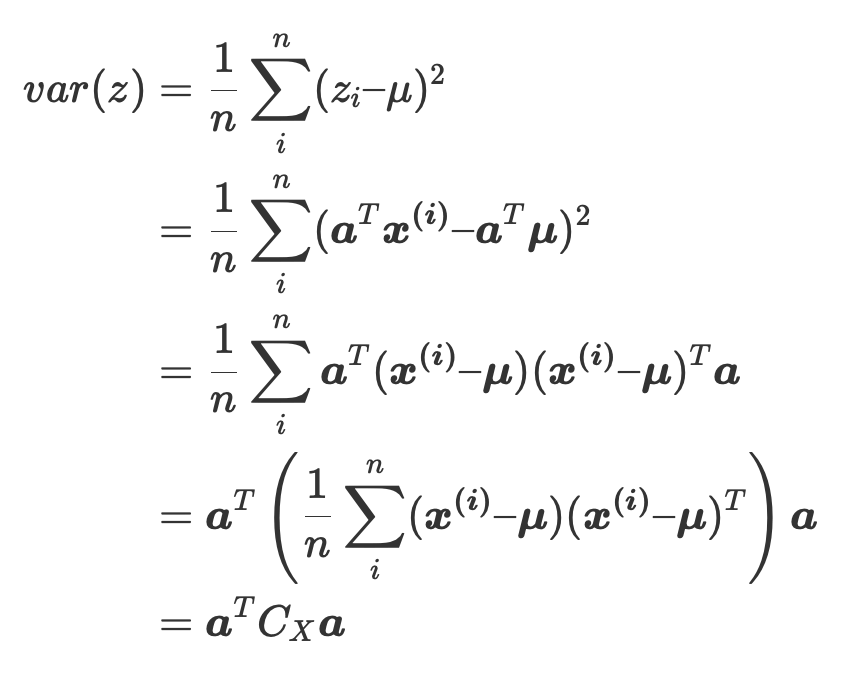

コメント