巡回セールスマン問題で有名な組み合わせ最適化問題は量子コンピュータの適用が注目される分野です。
しかし、量子コンピュータでも複雑な問題を高速かつ正確に解くのは容易ではありません。
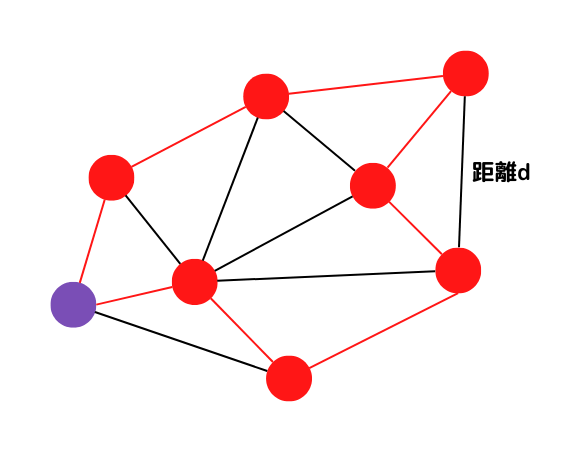
IBM Quantum Challenge2022 fallでは巡回セールスマン問題を効率的に解くための問題固有の量子回路の構築について取り上げられています。
本記事ではQuantum Challengeの内容に沿って量子コンピュータにおける組合せ最適化への取り組みについて紹介します。
量子コンピュータでも組み合わせ最適化は難しい
組合せ最適化の中には効率的に解けない(NP困難)問題があることが知られています。
巡回セールスマン問題もその一つです。

このような問題への解法は経験・発見的に妥当な解を時間内に計算する方法が唯一です。
経験・発見的なアプローチはヒューリスティックと呼ばれます。
ヒューリスティックの肝は、解の厳密さと計算コストのトレードオフです。
そして組み合わせ最適化問題の難点は、問題サイズに対して組み合わせが爆発することです。
下の動画を見ると組み合わせの爆発度合いがよくわかります。
つまり、量子コンピュータを使った並列計算が可能になっても、工夫をしない限りベストな答えにたどり着かないという課題があるのです。
実際にQuantum Challengeでは4ノードの巡回セールスマン問題が最適解に収束しないことが取り上げられています。
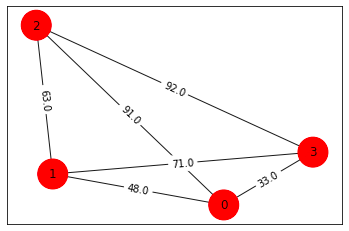
問題固有の制約を量子回路に取り入れる
爆発する計算コストを抑える工夫として、問題固有の制約を量子回路に導入して計算範囲を限定するアプローチが取り上げられています。
Quantum Challengeでは3ノード巡回セールスマン問題について、問題特有の制約を課した量子回路の実装が出題されています。
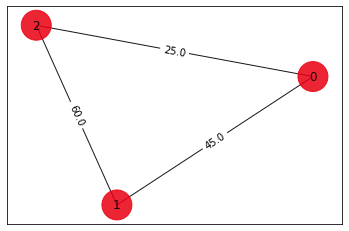
ここからは実際に量子回路の設計について考えていきましょう。
巡回セールス問題で考慮すべき制約は以下の2つです。
- どの都市も必ず1度は通る(以降「列制約」と呼びます)
\sum_p x_{i,p} = 1, \forall i- 各ステップではいずれか1つの都市にいる(以降「行制約」と呼びます)
\sum_i x_{i,p} = 1, \forall p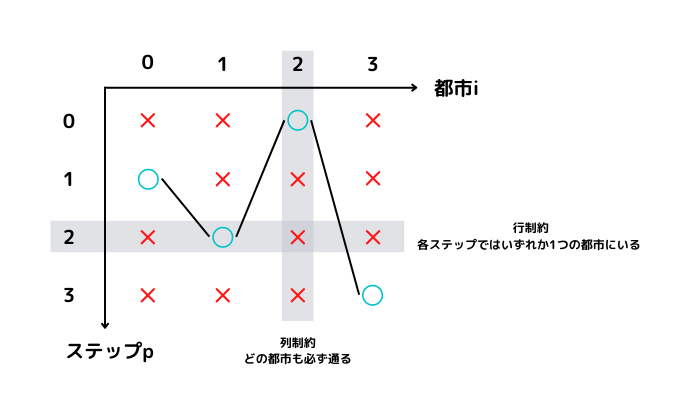
では上の2つの制約を量子回路に順番に導入していきます。
①列制約の導入
まずは列制約のみを考慮した問題特化型の量子回路を作ります。
\sum_p x_{i,p} = 1, \forall iこの条件を満たす解は$N^2$量子ビットのW状態という下記の形式で表せることができます。
巡回セールスマン問題では$p(1,\cdots,N)$ステップで都市$i(1,\cdots,N)$が巡回路であるかが変数となるので量子ビットは変数の数$N^2$だけ必要となります。
|W(\phi)\rangle = \sum_i \alpha_{i(\phi)} |\psi_i\rangle \\
|\psi_i\rangle \in \{|0\cdots01\rangle, \cdots,|10\cdots0\rangle\}列制約は同一の都市$i$に関してのみ制約をかけるので、W状態を作る量子回路は各$i$のグループごとに構成されるはずです。

各グループにおけるW状態を生成する量子回路は以下の回路で可能であることが元論文で提示されています。(以降W状態ゲートと呼びます。)
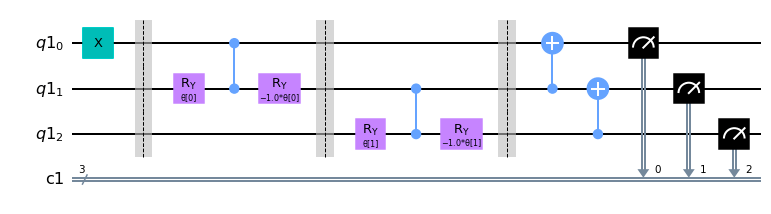
from qiskit import QuantumRegister, ClassicalRegister
from qiskit.circuit import ParameterVector, QuantumCircuit
# Initialize circuit
qr = QuantumRegister(3)
cr = ClassicalRegister(3)
circuit = QuantumCircuit(qr,cr)
# Initialize Parameter with θ
theta = ParameterVector('θ', 2)
circuit.x(0)
circuit.barrier()
circuit.ry(theta[0],1)
circuit.cz(0,1)
circuit.ry(-theta[0],1)
circuit.barrier()
circuit.ry(theta[1],2)
circuit.cz(1,2)
circuit.ry(-theta[1],2)
circuit.barrier()
circuit.cx(1,0)
circuit.cx(2,1)
# Apply gates to circuit
circuit.measure(qr,cr)
circuit.draw("mpl")したがって量子回路全体は下のようになります。
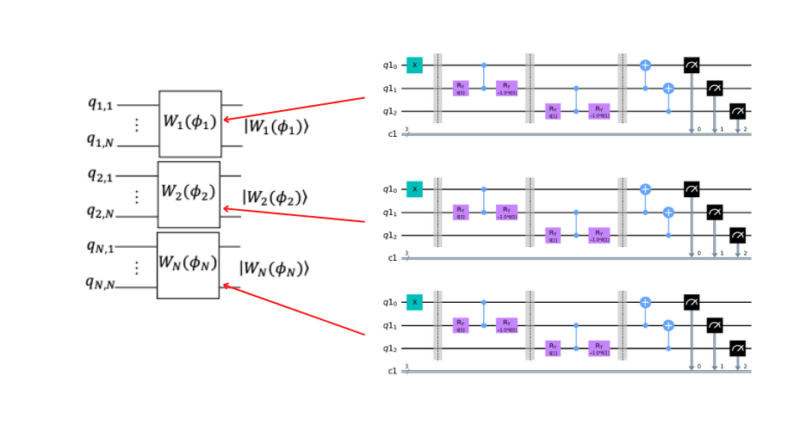
from qiskit import QuantumRegister, ClassicalRegister
from qiskit.circuit import ParameterVector, QuantumCircuit
def tsp_entangler(N):
# Define QuantumCircuit and ParameterVector size
circuit = QuantumCircuit(N**2)
theta = ParameterVector('theta',length=(N-1)*N)
for node in range(N):
# X Gate
circuit.x(N*node)
# Parameter Gates
for parameter in range(N-1):
circuit.ry(theta[node*(N-1) + parameter], node*(N) + parameter+1)
circuit.cz(node*(N)+parameter, node*(N) + parameter+1)
circuit.ry(-theta[node*(N-1) + parameter], node*(N) + parameter+1)
# CX gates
for parameter in range(N-1):
circuit.cx(node*(N) + parameter+1, node*(N) + parameter)
return circuit
tsp_entangler(3).draw("mpl")②列制約+一部の行制約を導入
続いて考慮する制約を加えて解の探索範囲をさらに限定します。
行制約を1つだけ導入します。つまり最初のステップでいずれか1つの都市にいるという制約です。
先程は量子回路を都市$i$毎に$N$グループに分けて考えましたが、今度は各グループの先頭の量子ビット同士に制約をかけます。
量子回路は下のように2つのパートで構成されます。
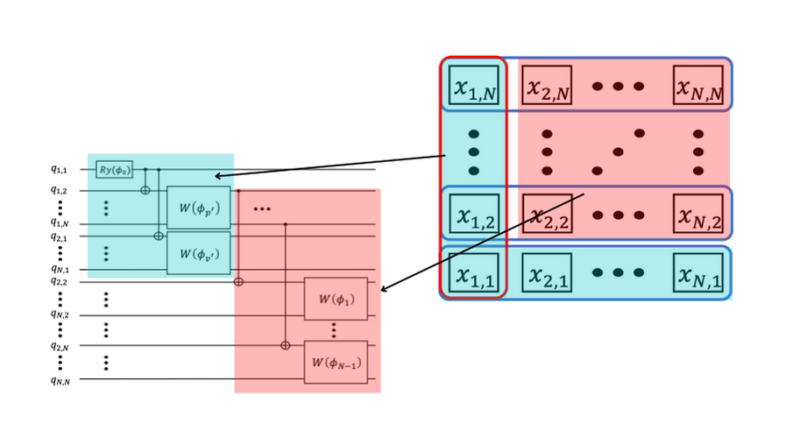
まずは青色の範囲の制約を実現する量子回路を考えます。この範囲の制約は以下のようにまとめることができます。
- $x_{1,1}=0$の場合、{$x_{1,p}$}と{$x_{i,1}$}それぞれのいずれか1つの変数は1
- $x_{1,1}=1$の場合、{$x_{1,p}$}と{$x_{i,1}$}いずれの変数も0
$x_{1,1}=0$の場合は先程のW状態ゲートが適用できそうです。
ここでW状態ゲートを振り返ると先頭の量子ビットの初期状態が1の場合、入力と出力は同じになります。つまり何もしないのと同じです。

したがって、CNOTゲートとW状態ゲートを組み合わせることで青色の制約を満たすことができます。
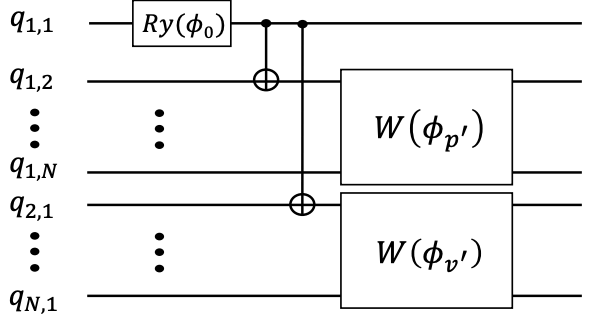
続いて赤色の制約を考えると、青色の制約とほぼ同じ構造を持つことがわかります。
- $x_{1,p}=0$の場合、{$x_{i,p}$}のいずれか1つの変数は1
- $x_{1,p}=1$の場合、{$x_{i,p}$}のいずれの変数も0
先程と同様に、CNOTゲートとW状態ゲートを組み合わせることで赤色の制約も満たすことができます。
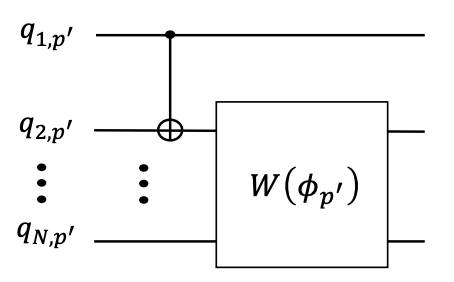
以上をまとめると3ノードの量子回路の全体像は下のようになります。
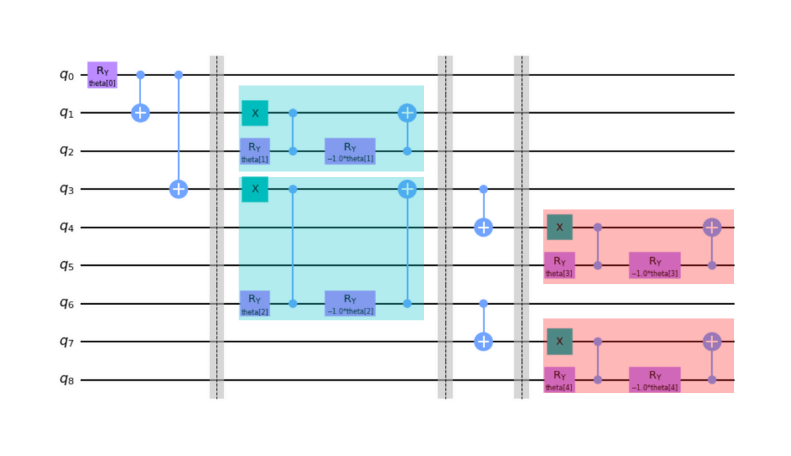
from qiskit import QuantumRegister, ClassicalRegister
from qiskit.circuit import ParameterVector, QuantumCircuit
n = 3
"""
Encode L shaped constraint
"""
l_circuit = QuantumCircuit(n**2)
theta = ParameterVector('theta',length=(n-1)*n-1)
# L-Shaped Entangler
l_circuit.ry(theta[0],0)
l_circuit.cx(0,1)
l_circuit.cx(0,3)
l_circuit.barrier()
#W_phi_p
l_circuit.x(1)
l_circuit.ry(theta[1],2)
l_circuit.cz(1,2)
l_circuit.ry(-theta[1],2)
l_circuit.cx(2,1)
#W_phi_v
l_circuit.x(3)
l_circuit.ry(theta[2],6)
l_circuit.cz(3,6)
l_circuit.ry(-theta[2],6)
l_circuit.cx(6,3)
l_circuit.barrier()
"""
Encode the remaining constraints
"""
r_circuit = QuantumCircuit(n**2)
theta = ParameterVector('theta',length=(n-1)*n-1)
# Two blocks remaining for N = 3
# Block 1 ---------
r_circuit.x(4)
r_circuit.ry(theta[3],5)
r_circuit.cz(4,5)
r_circuit.ry(-theta[3],5)
r_circuit.cx(5,4)
# Block 2 ---------
r_circuit.x(7)
r_circuit.ry(theta[4],8)
r_circuit.cz(7,8)
r_circuit.ry(-theta[4],8)
r_circuit.cx(8,7)
"""
Bridge between L-shape and original entangler
"""
bridge_circuit = QuantumCircuit(n**2)
theta = ParameterVector('theta',length=(n-1)*n-1)
bridge_circuit.cx(3,4)
bridge_circuit.cx(6,7)
bridge_circuit.barrier()
"""
Join all the three circuits
"""
model_2 = QuantumCircuit(n**2)
theta = ParameterVector('theta',length=(n-1)*n-1)
model_2 = l_circuit.compose(bridge_circuit).compose(r_circuit)
model_2.draw("mpl")③全ての制約を導入
最後は全ての制約を量子回路に反映します。
$N=k$ノードの問題のための量子回路は$k^2$量子ビット回路となりますが、これは以下の手順で$k-1$ノードの回路から再帰的に求まることが元論文で提示されています。
- $k-1$量子ビット回路に対し、{$x_{k,p}$}と{$x_{i,k}$}に相当する合計$2k-1$量子ビットを加える。
- $x_{k,k}=1$となるように{$x_{i,k}$}の部分へW状態ゲートを適用する。
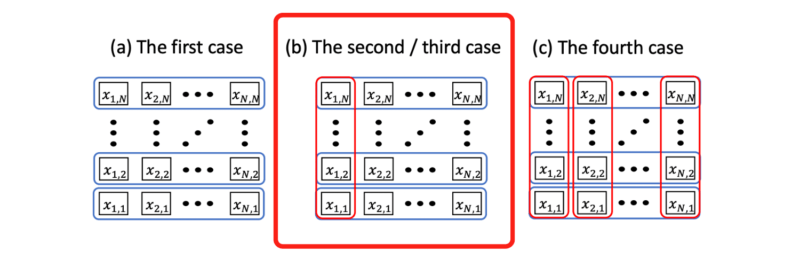
- {$x_{k,p}$}に相当する部分と{$x_{j,p}$}($j=1,\cdots,k-1$)に相当する部分を入れ替えの組み合わせを全て考慮する(下図)ためにCSWAPゲートを適用する。
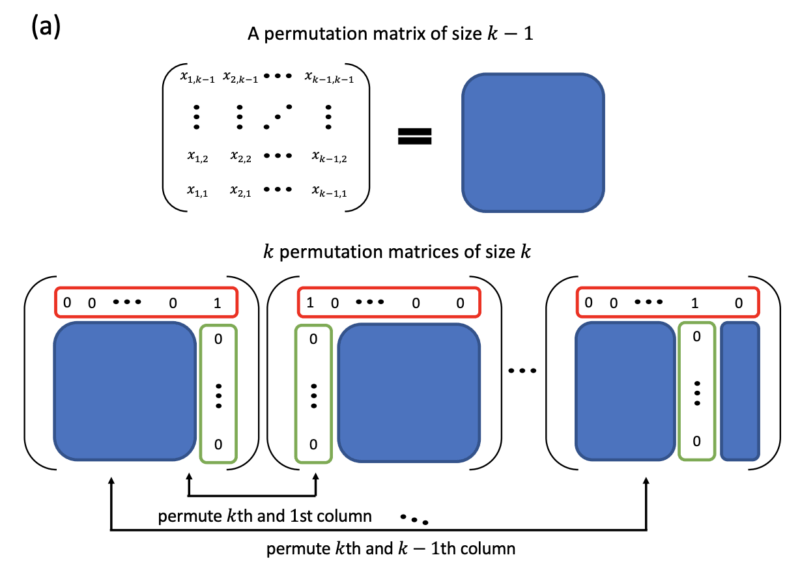
Quantum Challengeでは3ノード用の量子回路を求めることが問題となっているので実際に構築してみます。
まず最初の$N=2$の場合を考えます。解の候補は置換行列と呼ばれる下の2つであるとわかります。
\begin{bmatrix}
x_{1,2} & x_{2,2} \\
x_{1,1} & x_{2,1}
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
,
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}つまり出力される量子状態は2つの状態の重ね合わせとなるはずです。
|q_{1,1}q_{2,1}q_{1,2}q_{2,2}\rangle = \alpha_{1(\phi)}|1001\rangle + \alpha_{2(\phi)}|0110\rangleこのような状態は以下の量子回路で生成することができます。
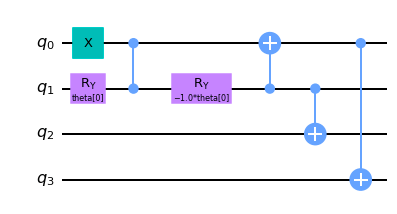
では$N=3$の量子回路を考えます。$N=2$の回路と先程の手順を踏まえると次のような回路を作ることができます。
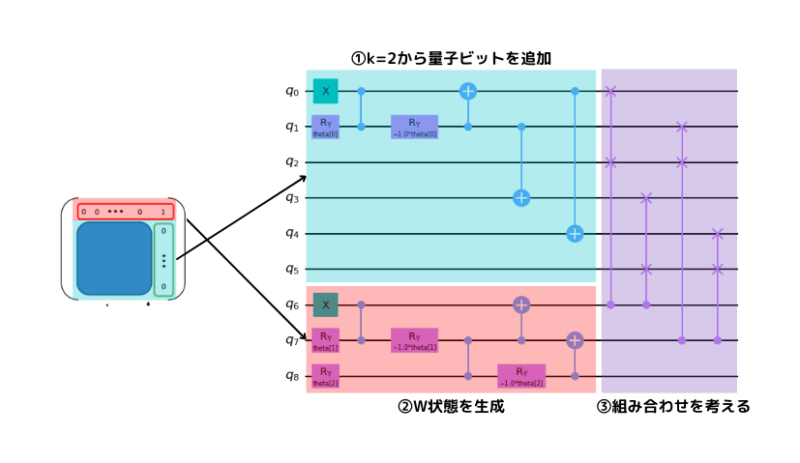
n = 3
model_3 = QuantumCircuit(n**2)
theta = ParameterVector('theta',length=(n-1)*n//2)
model_3.x(0)
model_3.ry(theta[0],1)
model_3.cz(0,1)
model_3.ry(-theta[0],1)
model_3.cx(1,0)
model_3.cx(1,3)
model_3.cx(0,4)
model_3.x(6)
model_3.ry(theta[1],7)
model_3.cz(6,7)
model_3.ry(-theta[1],7)
model_3.ry(theta[2],8)
model_3.cz(7,8)
model_3.ry(-theta[2],8)
model_3.cx(7,6)
model_3.cx(8,7)
model_3.cswap(6, 0, 2)
model_3.cswap(6, 3, 5)
model_3.cswap(7, 1, 2)
model_3.cswap(7, 4, 5)
model_3.draw("mpl")これで全ての制約を考慮した問題特化の量子回路を構築することができました。
3ノードの巡回セールス問題を解く
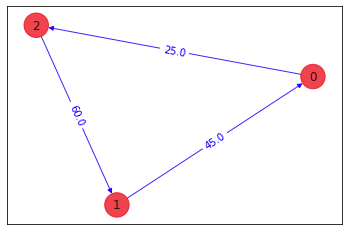
構築した3つの問題特化量子回路を用いて3ノードの巡回セールスマン問題の解を計算します。
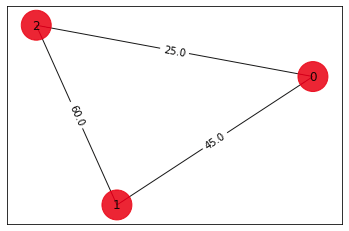
解は計算するまでもないですが、最適化計算を行います。
計算の詳細はQuantum ChallengeのExcersise6, 7に実装が記載されているので自分で実装する場合は参照してください。
ここでは結果だけ見てみましょう。
パターン1
-------------------
Energy: -4750.85369976058
Tsp objective: 130.14630023942027
Feasibility: True
Solution Vector: [1, 0, 2]
Solution Objective: 130.0
-------------------
パターン2
-------------------
Energy: -4750.997159699884
Tsp objective: 130.00284030011608
Feasibility: True
Solution Vector: [1, 0, 2]
Solution Objective: 130.0
-------------------
パターン3
-------------------
Energy: -4751.000000000002
Tsp objective: 129.99999999999818
Feasibility: True
Solution Vector: [1, 2, 0]
Solution Objective: 130.0
-------------------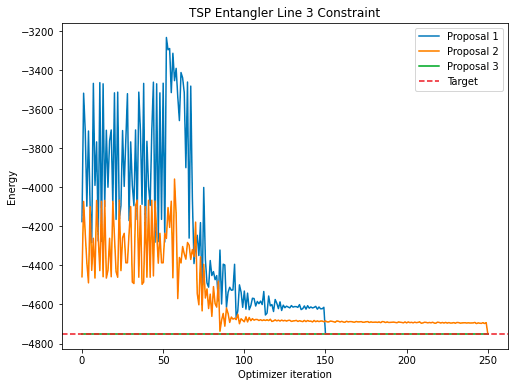
全パターンで右回り・左回りの差はあるものの、出力結果のSolution Vectorも最適解となっていることがわかります。
次にコスト関数の収束の様子を見ると、制約を強くかけるほど最適解周辺で探索を行っています。計算コストを抑えてより効率的に解を求められることがわかりました。
パターン1より2のほうが最終的な収束が遅い理由は不明です。
まとめ
この記事ではIBM Quantum Challenge2022 fallを題材に、問題特化の量子回路を構築して3ノード巡回セールスマン問題の解を効率的に求める方法を紹介しました。
Challengeではさらに4ノードの場合の解を求める設問が用意されています。

4ノードになると解が自明でない、かつ問題特化の量子回路を用いないと正しく収束しないので、今回のアプローチの威力をより実感出来ると思うのでぜひ取り組んでみてください。








コメント