Qiskit Textbookの新版が公開され、新たにQuantum machine learningの章が追加されたので紹介していきます。
今回紹介するのはParameterized Quantum Circuit(パラメータ化された量子回路)のセクションです。
中でもメイントピックと思われるParameterized quantum circuit propertiesについて扱います。
パラメータ化された回路とは
パラメータ化された回路とはその名の通り量子回路に調整可能なパラメータを用いたゲートを含む量子回路のことです。
直近のアプリケーションとして期待されているNISQ(Noisy Intermediate-Scale Quantum device)アルゴリズムの根幹を担っている概念になります。
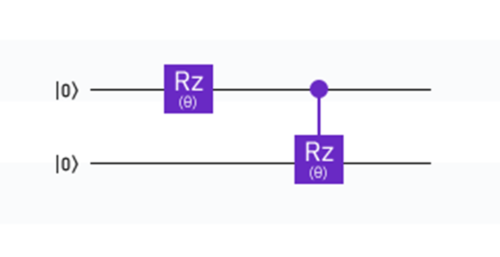
パラメータ化された回路の特徴づけ
テキストでは具体的な量子アルゴリズムについてではなく、より一般的に無数に考えられる量子回路の中からどのように最適な回路を探し出すかという観点を紹介しています。
そのためにパラメータ化された量子回路を定量的に評価するための指標を導入する必要があるとして、参考文献1(Sim et al, 2019)では以下の二つの指標を導入しています。
- Expressibility(表現能力)
- Entangling Capability(エンタングリング能力)
Expressibility(表現能力)
Expressibilityとは量子回路から生成される状態がブロッホ球(ヒルベルト空間)のどれだけをカバーできるかを定量化したものになります。
テキストでは下のように2つの1量子ビット回路を用いて回路から生成される状態2000サンプルをブロッホ球上にマッピングしたものを使ってExpressibilityの比較を表現しています。
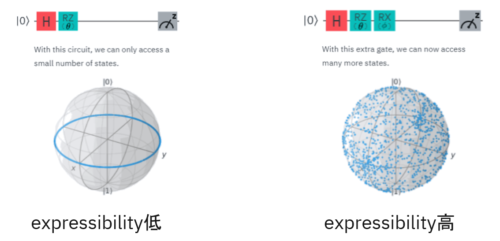
左の回路はZ軸回転ゲートがパラメータ$\theta$を持っているので、生成される状態はブロッホ球の赤道上に集中しています。
一方で右の回路はZ軸回転ゲートに加えてX軸回転ゲートが存在して、2つ目のパラメータ$\phi$を持っているので生成される状態はブロッホ球の全域をカバーしています。
Expressibilityはブロッホ球をどれだけカバ―出来るかという値なので、上の例では左の量子回路のExpressibilityは低く、右の回路は高いと評価することが出来ます。
ブロッホ球をカバーするほど様々な表現が可能となるため一般的にExpressibilityは高い方が使い勝手がよいという解釈になると思います。
Entangling Capability(エンタングリング能力)
Entangling Capabilityとは量子回路から生成される状態がどれだけエンタングルされた状態かを表す値です。
ここでは非常に簡単に複数量子ビットゲートが量子回路内に存在する場合はエンタングルメントの可能性ありとします。
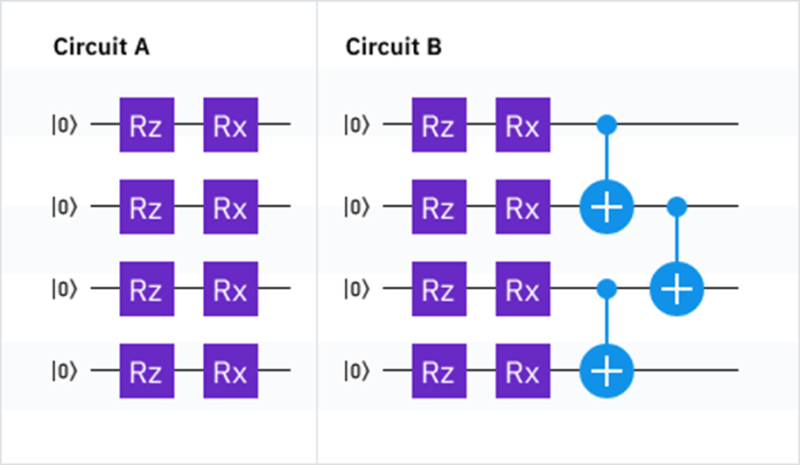
その視点でテキストの2つの量子回路を比較してみます。
左の回路Aは全て1量子ビットの回転ゲートのみで複数量子ビットゲートは存在しません。つまり複数の量子ビットを関連付ける操作が発生しないためエンタングルメントは発生しません。よってEntangling Capabilityは0となります。
一方回路Bは2量子ビットゲートであるCNOTゲートが存在しているためエンタングルメントは発生する可能性があり、Entangling Capabilityは0より大きい値をとると評価することが出来ます。
量子回路の評価
ではExpressibilityとEntangling Capabilityは様々な量子回路においてどんな性質をもっていて、最終的にどのように評価されるのでしょうか?
量子回路に対する指標の変化
参考文献1では以下の19の量子回路について、レイヤーの数を変えながらExpressibilityとEntangling Capabilityの値を数値計算しています。

まずは各回路のExpressibilityの推移について見ていきます。下のグラフからパッと読み取れる点は2つです。
- レイヤーの数を増やすほど値が改善する
- 一定のレイヤー数を超えると値が飽和する
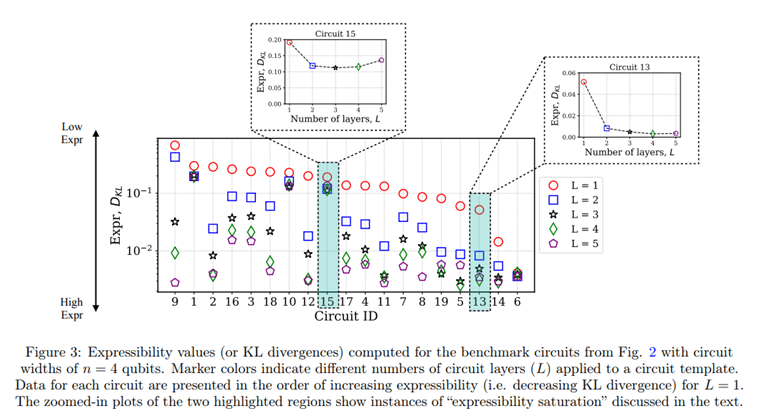
続いてEntangling Capabilityについてです。
- レイヤーの数を増やすほど値が改善する
- 少ないレイヤーでも高い値を示す場合はレイヤーを増やすと改悪する(例:回路9)
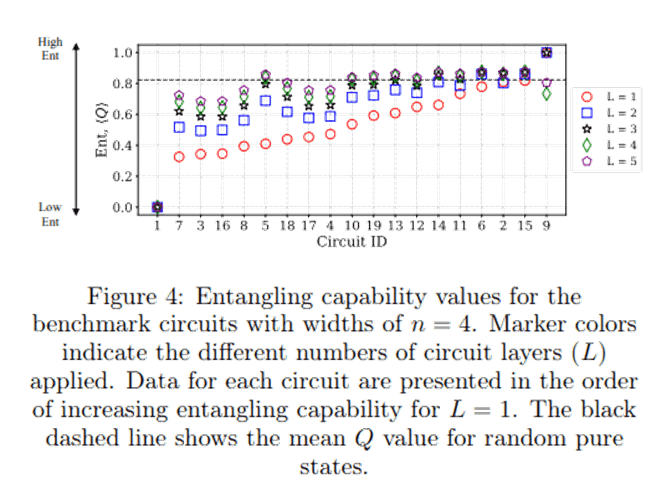
つまりまとめるとレイヤーを増やすほど回路は量子機械学習に適していくが、ある一定のレイヤーを超えるとそれ以上の効果は見込めないと言えると思います。
ただし、レイヤーを増やすほど回路の複雑度(回路の深さ、パラメータ数)が高くなるために計算に時間がかかる・複雑になることは注意しないといけません。シンプルである方が望ましいです。
量子回路の評価の例
以上を踏まえて論文では単層の量子回路について、Expressibility(縦軸)・Entangling Capability(横軸)・パラメータ数(色)の3軸でプロットした図を用いて量子回路の評価を行っています。
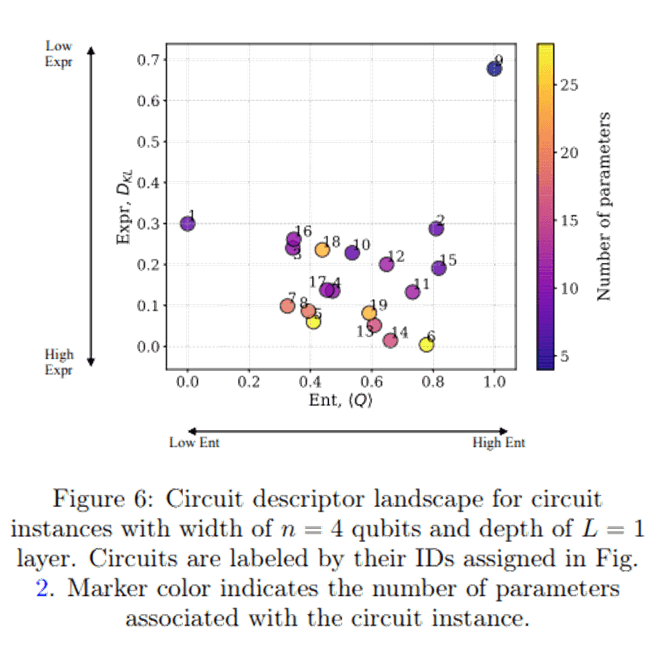
グラフの右下にいくほど回路の表現力は高く、古典コンピュータでは計算できない複雑な状態を作り出すことが出来るので量子機械学習への適用に適しているといえます。
そのように考えると今回の例では回路6が適切であるように見えます。
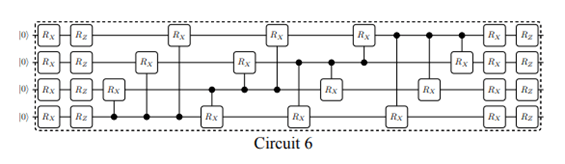
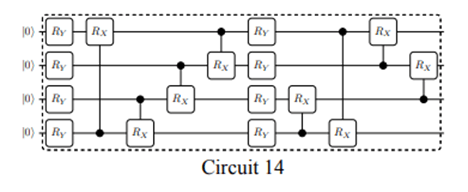
ただし回路6はパラメータ数がかなり多いので、そのコストをふまえると回路14が妥当な選択になるのかもしれない、このような形で回路を評価していくことになります。
まとめ
以上を今回の章をまとめると以下のようになります。
- パラメータ化された量子回路はExpressibilityとEnangling Capabilityの2つの指標で定量化可能
- Expressibilityはブロッホ球のカバレッジを示す値
- Entangling Capabilityはエンタングルメント状態の生成度合い
- 回路を深くするほど2つの指標はより量子機械学習に適するが、一定以上深くしても効果はない
今回の内容はConpassのイベントに登壇して話した内容をまとめたもので、Quantum TokyoのYoutubeチャンネルの動画にも上がっているので合わせてご覧ください!








コメント