量子コンピュータの応用先として期待されている機械学習の分野では、モデルの学習に何らかの最適化計算が行われますが、最適化の手法の中には関数の勾配情報を扱うものが多数存在します。
量子コンピュータで関数の勾配を求める手法はいくつかありますが、この記事ではパラメータシフト法という手法について、計算とQiskitによる実装の方法について解説します。
パラメータシフト法とは
パラメータシフト法とはパラメータ$\theta$の目的関数$\langle H(\theta)\rangle$の勾配を以下の計算式で求めることが出来るという計算手法です。
\frac{d\langle H(\theta)\rangle}{d\theta}=\frac{1}{2}(\langle H(\theta+\frac{\pi}{2})\rangle-\langle H(\theta-\frac{\pi}{2})\rangle)目的関数はVQEのアルゴリズムにおいてはエネルギー期待値とみなせます。
この手法は上の式を見ると単純な差分法によく似ていますが、パラメータを大きくシフトさせて差分を取るため差分法よりも誤差に堅牢であるという特徴があります。
\frac{d\langle H(\theta)\rangle}{d\theta}\sim\frac{1}{2h}(\langle H(\theta+h)\rangle-\langle H(\theta-h)\rangle)勾配の導出
では上の式がどのように導出されるかを確認していきましょう。例としてVQEにおいてエネルギー期待値のパラメータ微分を求めることを考えます。
仮定として試行状態を作る量子回路を1量子ビットの回転ゲートの形で表されるとします。
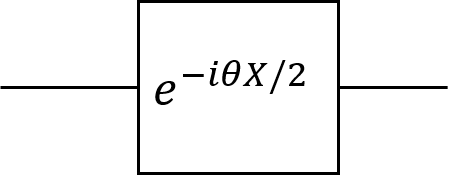
この時エネルギー期待値は次のように表されます。
\langle H(\theta)\rangle = \langle\psi|H|\psi\rangle = \langle0|e^{i\theta X/2}He^{-i\theta X/2}|0\rangleよってこれを$\theta$で微分すると下のように書けます。
\frac{d\langle H(\theta)\rangle}{d\theta}=\frac{i}{2}(\langle0|Xe^{i\theta X/2}He^{-i\theta X/2}|0\rangle-\langle0|e^{i\theta X/2}He^{-i\theta X/2}X|0\rangle)この物理量はそのまま観測することが難しく、補助ビットを用いることでこの微分表式を直接評価できる手法が提示されています。しかし使用できる量子ビットに限りあるNISQデバイスにおいては補助ビットの数を極力減らしたいものです。
そこで、この式をパウリ演算子の性質を用いて変形してみます。
e^{-i\theta X/2} = \cos \frac{\theta}{2}I - i\sin \frac{\theta}{2}Xこの式を利用することで最初に載せた式を導くことが出来ます。
\frac{d\langle H(\theta)\rangle}{d\theta}=\frac{1}{2}(\langle H(\theta+\frac{\pi}{2})\rangle-\langle H(\theta-\frac{\pi}{2})\rangle)Qiskitで実装する
ではパラメータシフト法による勾配計算をQiskitで実装していきます。
例題としてQHACKという量子機械学習ハッカソンで出題された“Exploring Quantum Gradients”の問題で考えてみましょう。
QHACKはQiskitではなくPennylaneという別のライブラリを使用したハッカソンです。
問題は下図の3量子ビット回路から生成される状態におけるハミルトニアンの期待値の勾配を計算せよというものです。
H = Y\otimes I\otimes Z
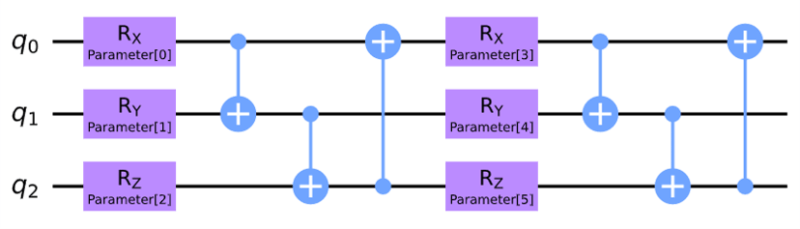
量子回路は以下のように生成可能です。
from qiskit.circuit import QuantumCircuit, ParameterVector
n = 3
qc = QuantumCircuit(n)
param_list = ParameterVector('Parameter', 2*n)
for i in range(len(param_list)//n):
qc.rx(param_list[3*i], 0)
qc.ry(param_list[3*i+1], 1)
qc.rz(param_list[3*i+2], 2)
qc.cnot(0, 1)
qc.cnot(1, 2)
qc.cnot(2, 0)
qc.draw(output='mpl')勾配計算にあたって、今回は2つのアプローチで実装していきます。
- ライブラリを利用しないで一から自分で実装する
- QiskitのGradient Frameworkを利用して実装する
入力パラメータは6つあるのでリストで渡します。
[1, 0.5, -0.765, 0.1, 0, -0.654]1から自分で実装する
ハミルトニアンの期待値を求めます。
from qiskit.opflow import StateFn, AerPauliExpectation
expectation = StateFn(hamiltonian, is_measurement=True) @ StateFn(qc)
pauli_basis = AerPauliExpectation().convert(expectation)from qiskit import Aer
from qiskit.utils import QuantumInstance
from qiskit.opflow import CircuitSampler
quantum_instance = QuantumInstance(Aer.get_backend('qasm_simulator'),
# we'll set a seed for reproducibility
shots = 32768, seed_simulator = 2718,
seed_transpiler = 2718)
sampler = CircuitSampler(quantum_instance)
def evaluate_expectation(params):
value_dict = dict(zip(qc.parameters, params))
result = sampler.convert(pauli_basis, params=value_dict).eval()
return np.real(result)続いて勾配を計算します。パラメータを$\pm \pi/2$だけシフトさせたハミルトニアンの期待値を計算してその差分を計算します。これを各パラメータ分計算します。
def calc_gradient(params):
gradient = np.zeros_like(params)
for i in range(len(params)):
shifted = params.copy()
shifted[i] += np.pi/2
forward = evaluate_expectation(shifted)
shifted[i] -= np.pi
backward = evaluate_expectation(shifted)
gradient[i] = 0.5 * (forward - backward)
return np.round(gradient, 10)結果を確認すると出力は期待値と一致していることが確認できました。
print(calc_gradient(input_param))
# > [ 0. 0. 0. 0. -0.45534747 0. ]
# 配布されている正解データ
[0, 0, 0, 0, -0.4553474723, 0]QiskitのGradient Frameworkを利用して実装する
以上の計算はQiskitが提供しているGradient Frameworkを利用することで先ほどよりも簡単に計算可能です。`Gradient`クラスを使用します。
from qiskit.opflow import Gradient
def calc_gradient_with_framework(params):
state_grad = Gradient(grad_method="param_shift").convert(operator=expectation)
value_dict = dict(zip(qc.parameters, params))
result = state_grad.assign_parameters(value_dict).eval()
return np.round(np.array(result).real, 10)出力結果は先程と同じく期待された結果を得ることが出来ました。
print(calc_gradient_with_framework(input_param))
# > [ 0. 0. 0. 0. -0.45534747 0. ]まとめ
パラメータシフト法を用いることで量子回路上で関数の勾配を計算することが出来ました。この手法は期待値を評価する量子回路をそのまま用いて評価が可能という点で特徴的です。
さらにこの手法はより一般の場合についても拡張が可能なことが知られています。詳しくはこちらをご覧ください。
今回掲載したソースコードは私のGitHubリポジトリでも公開しているので全体をご覧になりたい方はこちらにアクセスしてください。








コメント