Deutch-Jozsaアルゴリズムは量子計算が古典計算よりも高速に解を求めることができると提示された最初の例であり、量子計算の有用性を理解する上でよい例題となっています。
Deutschの問題
Deutch-Jozsaアルゴリズムとは以下のDeutchの問題を解くためのアルゴリズムとして考案されたものです。
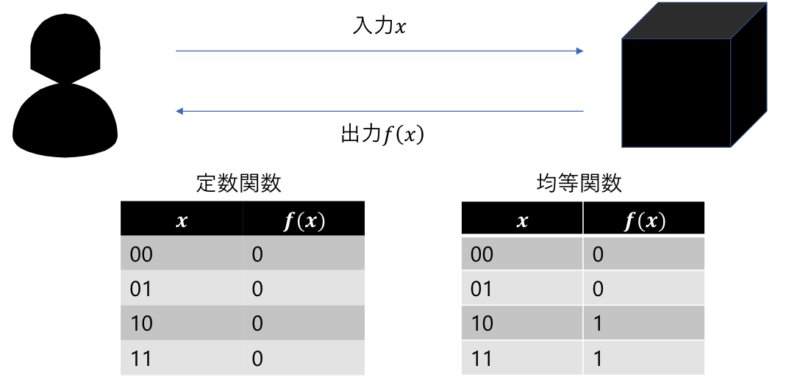
中身がわからないが、入力に対して演算を行って出力を返すブラックボックスの関数がある状況を考えます。関数は下のどちらかであることはわかっています。
- 定数関数:全ての入力に対して一定の値(0か1)を返す
- 均等関数:半分の入力に対しては0、半分の入力に対しては1を返す
このとき何回出力を確認すれば関数の性質を判定できるでしょうか?
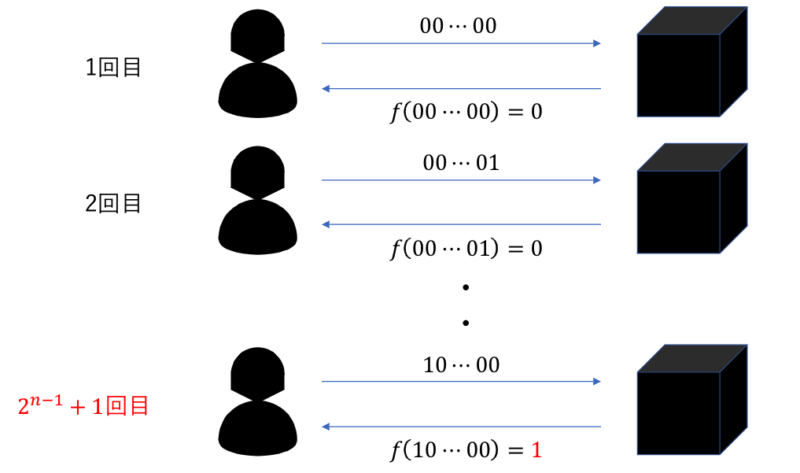
古典計算の場合は総当り方式で出力を確認して関数の性質を判定します。例えばnビットの入力を考えると、入力の組み合わせは$2^n$通り考えられます。
最も早く関数を判定できるのは1回目に出力0を得て2回目に出力1を得るような場合で、このときは2回の演算で関数を判定することができます。
一方で最悪の場合は$2^{n-1}$回目まで全て出力0を得て$2^{n-1}+1$回目に初めて出力1を得る場合です。古典計算でDeutschの問題を解こうとすると、最悪の場合は$2^{n-1}+1$回演算を行うまでは関数の判定ができません。
この問題を量子計算では1回の演算で関数の判別が可能となります。
量子計算のオラクルという考え方
量子計算で注意しないといけないのは計算過程が量子力学の法則に基づいている必要がある点です。その一つに量子計算は必ず可逆的、つまり出力から入力をたどることができる必要があります。
この観点で考えると特に全ての入力に対して定数を返す定数関数は可逆的ではありません。そこで演算が可逆的になるように量子計算では下のようなオラクルと呼ばれる関数を考えます。
$$ U_f|x\rang = |x \oplus f(x)\rang $$
オラクルに入力$|x\rang$を問い合わせて得られた結果は$|x\rang$の情報も含んでいるため演算を遡る事が可能な可逆的な演算とすることができました。
しかしこのままでは入力$|x\rang$を書き換えて出力を得ているため、補助ビット$|y\rang$を用いて入出力どちらも得られるようにします。
$$ U_f|x\rang|y\rang = |x\rang|x \oplus f(x)\rang $$
量子アルゴリズムの文脈では補助ビットには$|-\rang$ビットが用いられます。$|-\rang$ビットを用いることでオラクルに問い合わせた結果は入力に$(-1)^{f(x)}$という状態全体の位相(グローバル位相)を変化させる項が付くだけとなり、計算の見通しが良くなるからです。
$$ U_f|x\rang|-\rang = (-1)^{f(x)}|x\rang|-\rang $$
Deutch-Jozsaアルゴリズムの手順
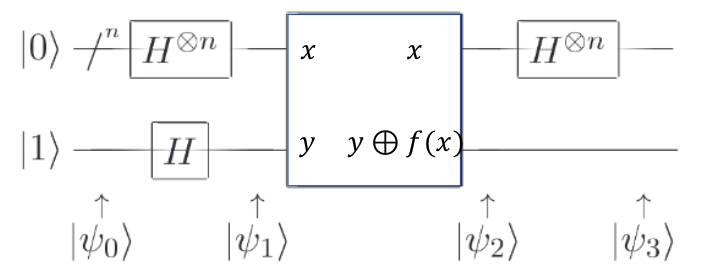
Deutch-Jozsaアルゴリズムでは重ね合わせ状態の量子ビットをオラクルに入力して結果を返してもらうことで高速な計算を可能としています。下がアルゴリズムの手順です。
上のnビットは入力ビット、下が補助ビットとなっています。補助ビットが$|1\rang$となっているのはアダマールゲートを作用させて上で説明した$|-\rang$を生成するためです。
- 入力用の𝑛量子ビットを全て$|0\rang$に初期化する
- 各量子ビットにアダマールゲートを作用させる(状態の重ね合わせを生成)
- オラクルに問い合わせる
- 再び各量子ビットにアダマールゲートを作用させる
- 各量子ビットを測定して関数を判定する
($|0\rang^{\otimes n}$なら定数関数、それ以外は均等関数)
例:入力が1ビットの場合
簡単な例として1ビットの入力を考えます。このとき$|\psi_0\rang$は下のように表すことができます。
$$|\psi_0\rang = |0\rang|1\rang$$
次に各ビットにアダマールゲートを作用させます。
$$|\psi_1\rang = \frac{1}{\sqrt(2)}(|0\rang + |1\rang)|-\rang$$
続いてオラクルに問い合わせをします。補助ビットは$|-\rang$なので結果は以下のように表すことができます。
$$\begin{aligned}|\psi_2\rang &= U_f\frac{1}{\sqrt(2)}(|0\rang + |1\rang)|-\rang \\ &= (-1)^{f(x)} \frac{1}{\sqrt(2)}(|0\rang + |1\rang)|-\rang \end{aligned}$$
ここで入力が1ビットの場合、$f(0) = f(1)$の場合定数関数、$f(0) \neq f(1)$の場合均等関数となります。以上を踏まえて再びアダマールゲートを作用させると以下のように表すことができます。
$$\begin{aligned}|\psi_3\rang &= \begin{cases} |0\rang|-\rang \text{ if } f(0) = f(1) \\ |1\rang|-\rang \text{ if } f(0) \neq f(1)\end{cases} \\ &= |f(0)\oplus f(1)\rang |-\rang \end{aligned}$$
したがって入力に用いた量子ビットを観測することで$|0\rang$のときは定数関数、$|1\rang$のときは均等関数と一度の問い合わせで判定することが可能です。これはnビットの入力においても同じことが言えます。($|0\rang^{\otimes n}$のときは定数関数)
まとめ
以上のようにDeutch-Jozsaアルゴリズムは量子の重ね合わせの性質を利用することで$2^{n-1}$回必要であった計算回数を1回にすることができるという、量子計算の有用性を認識するきっかけとなりました。







コメント