私達が普段使っているコンピュータは情報を0か1の組み合わせ(ビット列)で表現して、操作することで様々な計算を行っています。
ビットの考え方は量子コンピュータでも同様で、量子ビットという2つの量子の状態の違いを0と1の情報として表現します。

ここで厄介なのは計算途中の量子状態は確認できないということです。量子は状態を観測して確定してしまうと情報が壊れてしまう不思議な性質を持っているためです。
とはいえ計算途中が分からないと困るので、状態ベクトルやブロッホ球という量子状態を数学的に扱う考え方が導入されました。
この記事では状態ベクトルやブロッホ球の扱い方について紹介します。
状態ベクトルは量子状態の数学表現
状態ベクトルとは量子計算をベクトルの計算と考えることで、量子力学の法則に従いながら量子状態を数学的に表現したものです。
ベクトルとは大きさと方向を持った量です。方向を持つため普通の数(スカラー)と計算が多少異なります。
例えば$xy$座標におけるベクトルは下のように表されます。

赤の矢印は大きさが$\sqrt{1^2 + 1^2}=\sqrt{2}$、方向はx成分が1、y成分が1のベクトルであるといえます。
ベクトルを表す$|a\rangle$という記法は見慣れないと思いますが、状態ベクトルは慣例的にブラ・ケット記法という記法で表すと思ってください。
では先ほどのベクトル$|a\rangle$に下のようなベクトル$|b\rangle$を足してみましょう。
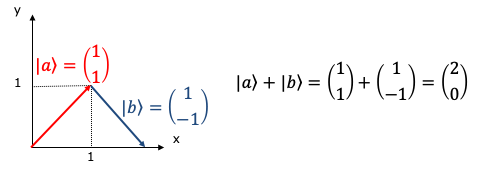
ベクトルの計算は各成分毎に行われるのでベクトル$|a\rangle$とベクトル$|b\rangle$の和はx成分が2、y成分が0のベクトルとなります。ここが普通の数(スカラー)の計算と大きな違いです。
量子状態は3次元空間でのベクトルで表現すると数学的に都合がいいというわけです。
状態ベクトルは0を表す状態$|0\rangle$と1を表す状態$|1\rangle$を基本単位とします。
量子特有の重ね合わせの状態ベクトル$|\psi\rangle$は基本ベクトルを用いて下記のように表すことができます。
|\psi\rangle = a|0\rangle + b|1\rangle
ブロッホ球は状態ベクトルを可視化
ブロッホ球は状態ベクトルを3次元球上で視覚化したものです。
状態ベクトルは数学的な制約を考慮すると3次元球で表現できてしまうのです。この点について確認してみます。
まず任意の量子状態は基本となる状態ベクトルの重ね合わせで次のように表すことができます。
|\psi\rangle = a|0\rangle + b|1\rangle
ここで注意したいのは、量子力学のルールとして$a^2+b^2=1$が必ず成り立つということです。
これは量子状態を数学的に表現すると、各状態の係数(確率振幅)の2乗はその状態が観測される確率を表し、その総和は必ず1となると量子力学が取り決めたためです。
この制約をパラメータ$\theta, \phi$を導入して別の形で表現します。
|\psi(\theta, \phi)\rangle = \cos \frac{\theta}{2}|0\rangle +e^{i\phi} \sin \frac{\theta}{2} |1\rangleこれは下図のように状態ベクトルが緯度$\theta$、軽度$\phi$の3次元球面の1点を指すことを表します。この3次元球がブロッホ球です。

状態ベクトルやブロッホ球を使うことで量子状態を可視化して追跡出来る点が大きな特徴です。
ブロッホ球の読み取り方
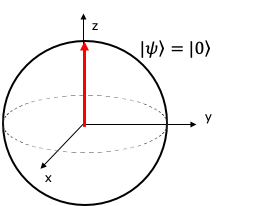
ブロッホ球では慣例的に$z$軸の上端を$|0\rangle$、下端を$|1\rangle$とします。
例えば状態ベクトルが$z$軸の上方向を指す時、量子状態は純粋に0の状態です。
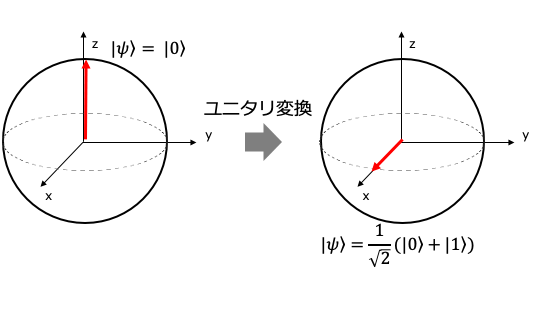
状態ベクトルが$x$軸方向を指す時は量子状態は重ね合わせで、0と1の状態のどちらかが確率50%で観測されます。
数学的には$\theta=\pi/2, \phi=0$なので次のように表されます。
|\psi\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
状態ベクトルやブロッホ球は量子状態を扱いやすくするために便宜的に考案されたもので、球そのものに意味はありません。このように表すと計算上都合がいいと割り切ってしまいましょう。
ブロッホ球上で量子計算や測定を考える
量子状態をブロッホ球で表現することで量子の計算や測定も可視化することができます。
量子計算は量子力学の枠組みの範囲内で行われる操作なので、演算後の量子状態も当然ブロッホ球上で表現されます。つまり量子計算はブロッホ球上で状態ベクトルの回転で表現することができます。
このような量子計算の操作をユニタリ変換といいます。
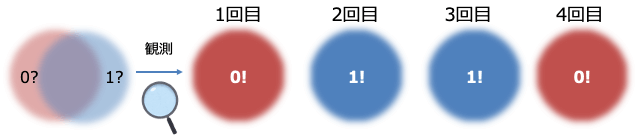
また測定は量子状態を0か1の状態のどちらかに確定する操作です。これはブロッホ球上で状態ベクトルのz軸方向の成分を取り出す射影操作と考えることができます。
ただし注意したいのは、実際に測定で得られる結果は測定ごとに変化します。
例えば$|\psi\rangle = (|0\rangle + |1\rangle)/\sqrt{2}$の量子状態を測定すると確率50%で0か1が観測されることになります。
まとめ
以上量子状態の可視化のための状態ベクトルとブロッホ球の紹介でした。
どんな量子操作も基本的にはブロッホ球の回転としてすべて表現することが出来るので、もし計算がわかりにくいといった場合は活用してください。
より詳しく学びたい方向けに
今回の内容はこちらの本を参考に書きました。
量子計算の上で最も基本的な概念になるので、これから数学をつかって量子コンピュータをしっかり勉強したいという方はぜひこちらの本を参考にしてください!
詳細のレビューも参考にしてみてください。








コメント