SPSA(Simultaneous Perturbation Stochastic Approximation)とは最適化手法の一つで、ランダムに選んだ方向の差分を取ることで、関数の勾配を近似する手法です。
\nabla f(\bm\theta) \simeq \frac{f(\bm \theta + \epsilon \bm \Delta) - f(\bm \theta - \epsilon \bm \Delta)}{2\epsilon}\bm \Delta^{-1} \\
ただし\epsilon\bm \Delta\{+1, -1\}^nSPSAは様々な量子アルゴリズムの最適化手法に採用されていますが、この記事ではその背景となるSPSAの特徴と、Qiskitを使って実際に実装する方法を紹介します。
SPSAの特徴
SPSAは以下のメリットがあることから特に量子機械学習でよく採用されている手法です。
計算コストが軽い
近似式を見ると、勾配の計算を関数値のみで表現しているため微分計算が複雑・そもそも微分不可能な関数においても利用できる点が大きな特徴です。
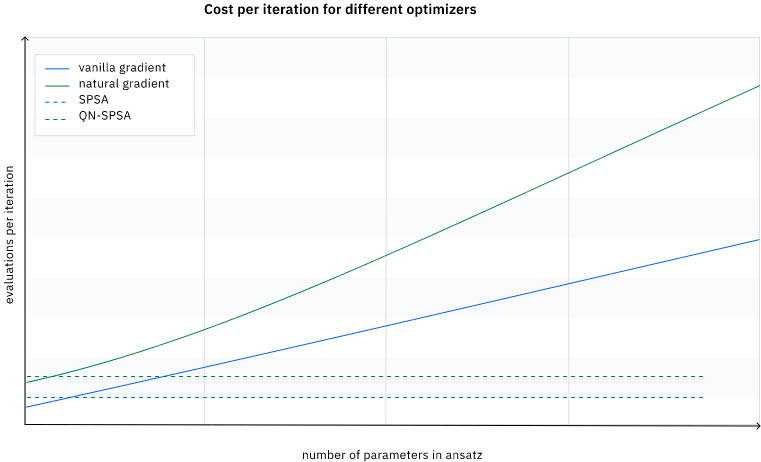
ただし、これはパラメータシフト法でも同様のことが言えます。SPSAが優れている点は関数の評価回数が少なく済むことにあります。
\begin{align}
\nabla f(\bm\theta)
&\simeq
\frac{1}{2\epsilon}\begin{pmatrix}
f(\bm \theta + \epsilon \bm e_1) - f(\bm \theta - \epsilon \bm e_1) \\
\cdots \\
f(\bm \theta + \epsilon \bm e_n) - f(\bm \theta - \epsilon \bm e_n)
\end{pmatrix}\\
&\simeq
\frac{f(\bm \theta + \epsilon \bm \Delta) - f(\bm \theta - \epsilon \bm \Delta)}{2\epsilon}\bm \Delta^{-1}
\end{align}(1)はパラメータシフト、(2)はSPSAの評価式になります。
(1)は各パラメータの方向ごとに勾配の近似計算を行うため、パラメータの数を$n$とすると勾配を求めるために$2n$個の関数値の評価が必要となります。
一方でSPSAではランダムな方向に対する近似値計算を行うため、関数値の評価はパラメータの数によらず2回です。
実際の最適化計算ではパラメータ更新の繰り返しの回数分だけ勾配計算を行う必要があるため、大規模な系ほどSPSAの計算コストの軽さが際立つことがわかります。
ノイズに対して堅牢
SPSAの2つ目のメリットは最適化計算がノイズに対して堅牢という点です。
量子コンピュータにおける関数値の評価は量子状態の測定が必要となるためノイズが混入します。
しかし、SPSAでは関数のパラメータに予めランダムな摂動を加えて評価しているため、ノイズが混入しても摂動に埋もれてしまいノイズの影響を受けにくいと考えられています。
Qiskitによる実装
それではQiskitで実装して動作を確認しましょう。SPSAはqiskit.algorithms.optimizersのモジュールを使用します。
実装は基本的に他のオプティマイザと同様にやることは3つです。
- モジュールのインポート
- コールバック処理の定義
- インスタンス化
- 最適化処理の実行
from qiskit.algorithms.optimizers import SPSA
spsa_loss= []
xx_op_spsa= []
yy_op_spsa= []
# コールバック処理の定義
def spsa_callback(nfevs, x, fx, stepsize, accepted):
spsa_loss.append(fx)
xx_op_spsa.append(x[0])
yy_op_spsa.append(x[1])
# インスタンス化
spsa = SPSA(maxiter=100,learning_rate=0.05,perturbation=0.05, callback=spsa_callback)
# 最適化処理の実行
x_opt_spsa, fx_opt_spsa, nfevs_spsa = (
spsa.optimize(initial_point.size,
calculate_exp_val,
initial_point=initial_point)
)動作を確認するために、以下の2量子ビットのパラメータ回路を用意します。
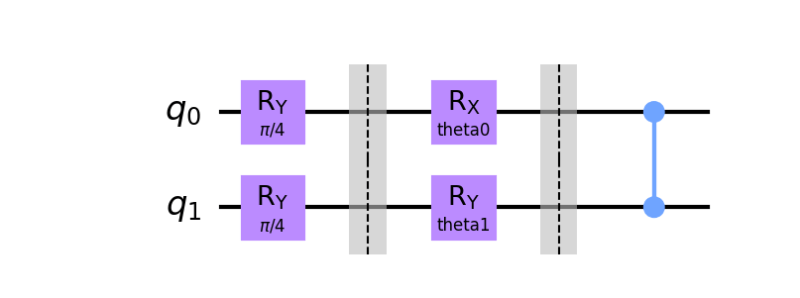
ここでコスト関数は以下のハミルトニアンの期待値を取ることにします。下のグラフは量子回路中のパラメータに対するコスト関数の値をプロットしたものになります。
\mathscr{H} = Z \otimes Z \\
loss = \langle\psi|\mathscr{H}|\psi\rangle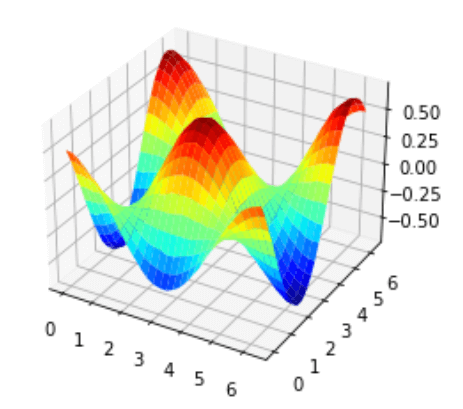
それではSPSAで最適化を行った結果を確認してみましょう。比較のため最急降下法で計算した結果も併せて描画しています。
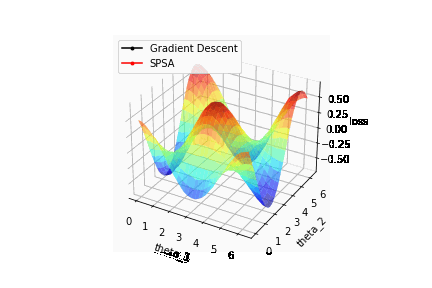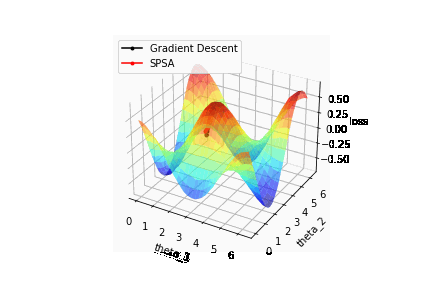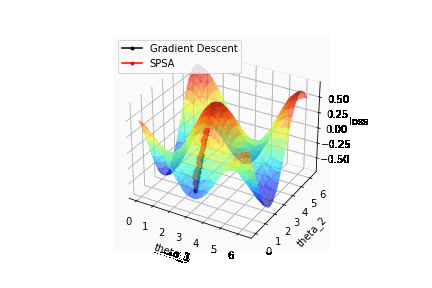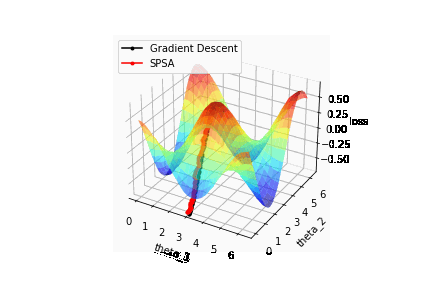
結果はSPSAと再急降下法の収束はほぼ同じことが確認できます。つまり計算コストを減らした状態でも最急降下法と同等のパフォーマンスを出すことが可能ということが確認できました。
またSPSAの計算結果がゆらゆらと揺れているのは、パラメータの更新をランダムな方向に取っているからに他なりません。そのためSPSAはあくまで収束に焦点を当てているため途中の結果がコスト関数と一致することは保証していません。
まとめ
この記事では量子機械学習でしばしば登場するSPSAという最適化手法について紹介しました。
- 他の手法と比較して計算コストが軽い(関数の評価回数が少ない)
- ノイズに対して堅牢なのでNISQデバイスでも適用が期待









コメント